Salesforce integrations can be tricky. One of our customers had to connect a system that required the use of JSON Web Tokens with an RSA-SHA512 signature.
One workaround was to implement the RSA cryptography in Apex. Let's see how the Apex language enables us to express a wide variety of solutions, even at the bare metal if needed.
| Update: the platform Crypto class now supports RSA-SHA512 signatures You should use native methods as of the Summer '20 release - Stronger hashing algorithms in Apex |
At its core, RSA (invented by Rivest / Shamir / Adleman) is a cryptosystem based on a mathematical trick and involves several moving parts. Apex source code on GitHub.
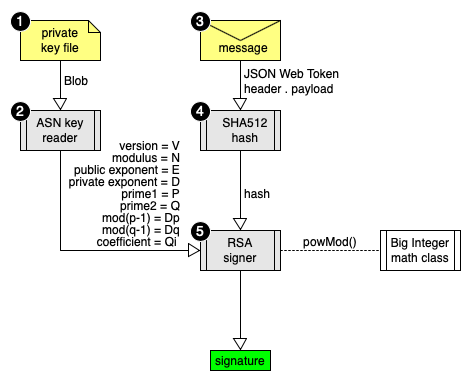
- A private key file holds secret prime numbers
- An ASN key reader handles the binary file format
- The message to sign consists of a JSON Web Token
- Then a SHA512 hash reduces the message to a big integer
- Finally the RSA signer executes the modPow signature math
To succeed, we must implement each logical part in Apex then make it performant. A similar look and feel to the platform Crypto class can be achieved starting with pseudocode like this:
Blob sign(Blob inputMessage, String privateKeyFile)
{
ASN reader = new ASN(privateKeyFile);
RSA signer = new RSA(reader.values());
return signer.sign(SHA512(inputMessage));
}Step 1) Private Key File
The signing process always starts with an RSA Private Key. For example, this RSA tool generates a binary representation of a private key wrapped in a header / footer. This is called a PEM file and it is base64 encoded to simplify transport by email or your clipboard:
-----BEGIN RSA PRIVATE KEY----- MIICXAIBAAKBgQCpIwKH7fYUgtCtOCtnvIlAXcFvzLPkLWWHNZoT+hOIzT WR+PrOQiQrat7wsVD+161g3CUUcdpTR2HMSThWxEjLldsZq0BA3TqEecXm V6rZzy0ZTJb2tgzjoX+eNiLvIHpgAaq5x2g2J9mB/b/9PFWspvQgMPAXl6 rpAM5ZNIEwuQIDAQABAoGBAKLMYP5HbMo3U/a3Dwhtr8p1s+ARr8FcdNId JO4/khfmNb8IYRixDzF/T5FriyOQo4CMxWAVamkoVxkUDRdvHQTO17hWMK ysLIn46y3bHxxRb6g5tpSwK61L25Hdiwi9GjqGrn7Z5rMFIqOqaCIX9gUQ ICmW31Y7XyekZ9RPA+8VAkEA39A2eqystpFTtkvfrAgG7uOL4IrckA5kuC 4xPHeehvlI8bDZU4kmLFNnduNOVtfKSxzfT4l+Qvl8IRxUycRodwJBAMF1 2s9NvILcJ1i2Ah2oTf91gkv82XoNOr0DsdLMqRkNSODKWiqxwZTVq8OeiW wF58FzdBmNJegVfoE2eO0zrE8CQH7B0KkHtMWtZwjeze4DmdGgQ+9HFgXs cPSzDKWfZcQx2TMxItSh32HJVtbJg+vBSUvjLUJBr6XE4J1sC0U+nJ8CQE /4eunk1X82qGEoY7mEwDFQjvsAW5nzbAuEQnbEOUZs0mpx21H4xu/SX71u hJoN2t6B7kU9rqTAddnN/bD4AksCQBuhIVld31iTzgyrc4R9e+KnLuW0rP /01SWYPYE0oeYCViZ/r19XsHQicPFLjKtKoOLNhVlHGsrW0yCnpcb2ahs= -----END RSA PRIVATE KEY-----
To work with individual bytes, convert the data into hexadecimals:
String b64 = 'MIICXAIB...'; Blob binary = EncodingUtil.base64decode(b64); String hex = EncodingUtil.convertToHex(binary);
Now with each byte seen as a hex pair, structure emerges:
3082025C02010002818100A9230287EDF61482D0AD382B67BC89405DC16FCCB3E42D6587359A 13FA1388CD3591F8FACE42242B6ADEF0B150FED7AD60DC251471DA534761CC493856C448CB95 DB19AB4040DD3A8479C5E657AAD9CF2D194C96F6B60CE3A17F9E3622EF207A6001AAB9C76836 27D981FDBFFD3C55ACA6F42030F01797AAE900CE59348130B9020301000102818100A2CC60FE 476CCA3753F6B70F086DAFCA75B3E011AFC15C74D21D24EE3F9217E635BF086118B10F317F4F 916B8B2390A3808CC560156A69285719140D176F1D04CED7B85630ACAC2C89F8EB2DDB1F1C51 6FA839B694B02BAD4BDB91DD8B08BD1A3A86AE7ED9E6B30522A3AA682217F60510202996DF56 3B5F27A467D44F03EF15024100DFD0367AACACB69153B64BDFAC0806EEE38BE08ADC900E64B8 2E313C779E86F948F1B0D95389262C536776E34E56D7CA4B1CDF4F897E42F97C211C54C9C468 77024100C175DACF4DBC82DC2758B6021DA84DFF75824BFCD97A0D3ABD03B1D2CCA9190D48E0 CA5A2AB1C194D5ABC39E896C05E7C17374198D25E8157E813678ED33AC4F02407EC1D0A907B4 C5AD6708DECDEE0399D1A043EF471605EC70F4B30CA59F65C431D9333122D4A1DF61C956D6C9 83EBC1494BE32D4241AFA5C4E09D6C0B453E9C9F02404FF87AE9E4D57F36A8612863B984C031 508EFB005B99F36C0B844276C439466CD26A71DB51F8C6EFD25FBD6E849A0DDADE81EE453DAE A4C075D9CDFDB0F8024B02401BA121595DDF5893CE0CAB73847D7BE2A72EE5B4ACFFF4D52598 3D8134A1E60256267FAF5F57B0742270F14B8CAB4AA0E2CD8559471ACAD6D320A7A5C6F66A1B
Step 2) Abstract Syntax Notation - ASN.cls
The private key file is not just a random seed. It holds 9 pieces of content in Tag-Length-Value encoding per Abstract Syntax Notation One. Reading each hex pair (or byte) as a string, Apex will extract the critical prime numbers (P, Q, etc) described in the RSA specification.
- Tag byte
- Length byte
- Contents bytes
The first tag tells us the data holds a list of values called a sequence:
| Hex | Type | Hex | Length |
|---|---|---|---|
| 30 | Sequence | 82025C﹡ | 604 bytes |
﹡When content length exceeds 128 bytes (hex 80) the length of the length is also given.
Here, hex 82 means a 2-byte length, then 025C means the sequence is 604 bytes long.
Let's tabulate all the subsequent values contained inside the sequence:
| Hex | Type | Hex | Length | Hex | Value |
|---|---|---|---|---|---|
| 02 | Integer | 01 | 1 byte | 00 | Version: V |
| 02 | Integer | 8181﹡ | 129 bytes | 00A92302… | RSA modulus: N |
| 02 | Integer | 03 | 3 bytes | 010001 | RSA public exponent: E |
| 02 | Integer | 8181﹡ | 129 bytes | 00A2CC60… | RSA private exponent: D |
| 02 | Integer | 41 | 65 bytes | 00DFD036… | Prime1: P |
| 02 | Integer | 41 | 65 bytes | 00C175DA… | Prime2: Q |
| 02 | Integer | 40 | 64 bytes | 7EC1D0A9… | Dp Exponent1: D mod (P-1) |
| 02 | Integer | 40 | 64 bytes | 4FF87AE9… | Dq Exponent2: D mod (Q-1) |
| 02 | Integer | 40 | 64 bytes | 1BA12159… | Coefficient: Qinv mod P |
﹡When content length exceeds 128 bytes (hex 80) the length of the length is also given.
Here, hex 81 means a 1-byte length, then 81 means the integer is 129 bytes long. Not bits.
Step 3) JWT Message - Tutorial
JSON Web Tokens exist to prove the integrity of an API request: only the private key holder can sign tokens and issue valid requests. Each token consists of three parts: Header / Payload / Signature. The special values are covered in depth in the tutorial.
Combine the Header and Payload to prepare the message:
String header = '{"alg":"RS512","typ":"JWT"}';
String payload = '{"iat":1581009850,"exp":1581011650}';
String message = base64url(header) + '.' + base64url(payload);Note the base64 URL variant strips trailing = padding, swaps + for -, and / for _ according to the JWT spec. This avoids issues if intermediate systems use tokens as filenames.
Step 4) Hash Function - SHA512.cls
Hashing the message ensures the input to the signature math is a predictable length. Else the signature math would become more and more expensive with each byte of data in the token.
Blob hashedMessage = Crypto.generateDigest('SHA-512', Blob.valueOf(message));Step 5) Signature - RSA.cls
The original concept of modular exponentiation underlying RSA was described in 1977 and (assuming small prime numbers) can be executed with pen and paper by hand in 10 minutes:
Signature = CD mod P×Q (for message C, private exponent D, primes P and Q)
Eddie Woo - The RSA Encryption Algorithm
In real situations, this modular exponentiation gets computationally expensive and exceeds the Apex CPU limit without using a specific optimization: the Chinese Remainder Theorem.
It isn't the end of the road. Most crypto libraries use the CRT optimization. In fact, its use is so common that ALL private keys hold 5 extra values, precomputed to help implement CRT. The implementation in Apex can be seen as a direct parallel of the algorithm from Wikipedia:
| Chinese remainder theorem (Wikipedia) | Apex implementation in RSA.cls |
| m1 = CDp mod P m2 = CDq mod Q h = Qinv (m1 - m2) mod P m = m2 + HQ mod PQ |
M1 = C.powMod(Dp, P); M2 = C.powMod(Dq, Q); H = Qinv.multiply(M1.subtract(M2)).mod(P); M = M2.add(H.multiply(Q).mod(P.multiply(Q))); |
Big Integer math class - BigInt.cls
All the aforementioned math must work with big integers. The calculations must be exact and this is where the real challenge lies. Back in Step 2 you probably spotted the 129-byte value in the private key. That number has 300+ digits while the maximum length of any number in Apex is 19 digits. This isn't a shortcoming of Apex - most languages have the same constraint. An extra class handles the big integers, representing them as lists of smaller integer primitives.
Acknowledgements
This solution stands of the shoulders of a number of people who provided reference implementations and ideas. We wish to express appreciation for their published work:
- RSA key utility by Kenju Urushima https://github.com/kjur/jsrsasign
- ASN.1 parser by Lapo Luchini https://github.com/lapo-luchini/asn1js
- BIG INTEGER math by Tom Hu http://www-cs-students.stanford.edu/~tjw
- SHA512 message digest by Michael Tritton https://github.com/trittimo/SHA512

